플로이드-워셜 알고리즘(Floyd-warshall)
- 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산하는 알고리즘
- 2차원 테이블에 최단 거리 정보를 저장한다.
- 다이나믹 프로그래밍 유형에 속한다.
- 각 단계마다 특정 노드 k를 거쳐 가는 경우를 확인하여 a-b의 최단 거리보다 a-k-b가 짧은지 검사한다.
플로이드-워셜 알고리즘 문제
1956번: 운동
첫째 줄에 V와 E가 빈칸을 사이에 두고 주어진다. (2 ≤ V ≤ 400, 0 ≤ E ≤ V(V-1)) 다음 E개의 줄에는 각각 세 개의 정수 a, b, c가 주어진다. a번 마을에서 b번 마을로 가는 거리가 c인 도로가 있다는 의
www.acmicpc.net
import sys
#플로이드 워셜
input = sys.stdin.readline
v,e = map(int, input().split())
INF = int(1e9)
graph = [[INF] *(v+1) for _ in range(v+1)]
for _ in range(e):
a,b,c = map(int, input().split())
graph[a][b] = c
for k in range(1, v+1):
for i in range(1, v+1):
for j in range(1, v+1):
graph[i][j] = min(graph[i][j] , graph[i][k]+graph[k][j])
rst = INF
for i in range(1,v+1):
rst = min(rst, graph[i][i])
if rst ==INF:
print(-1)
else:
print(rst)
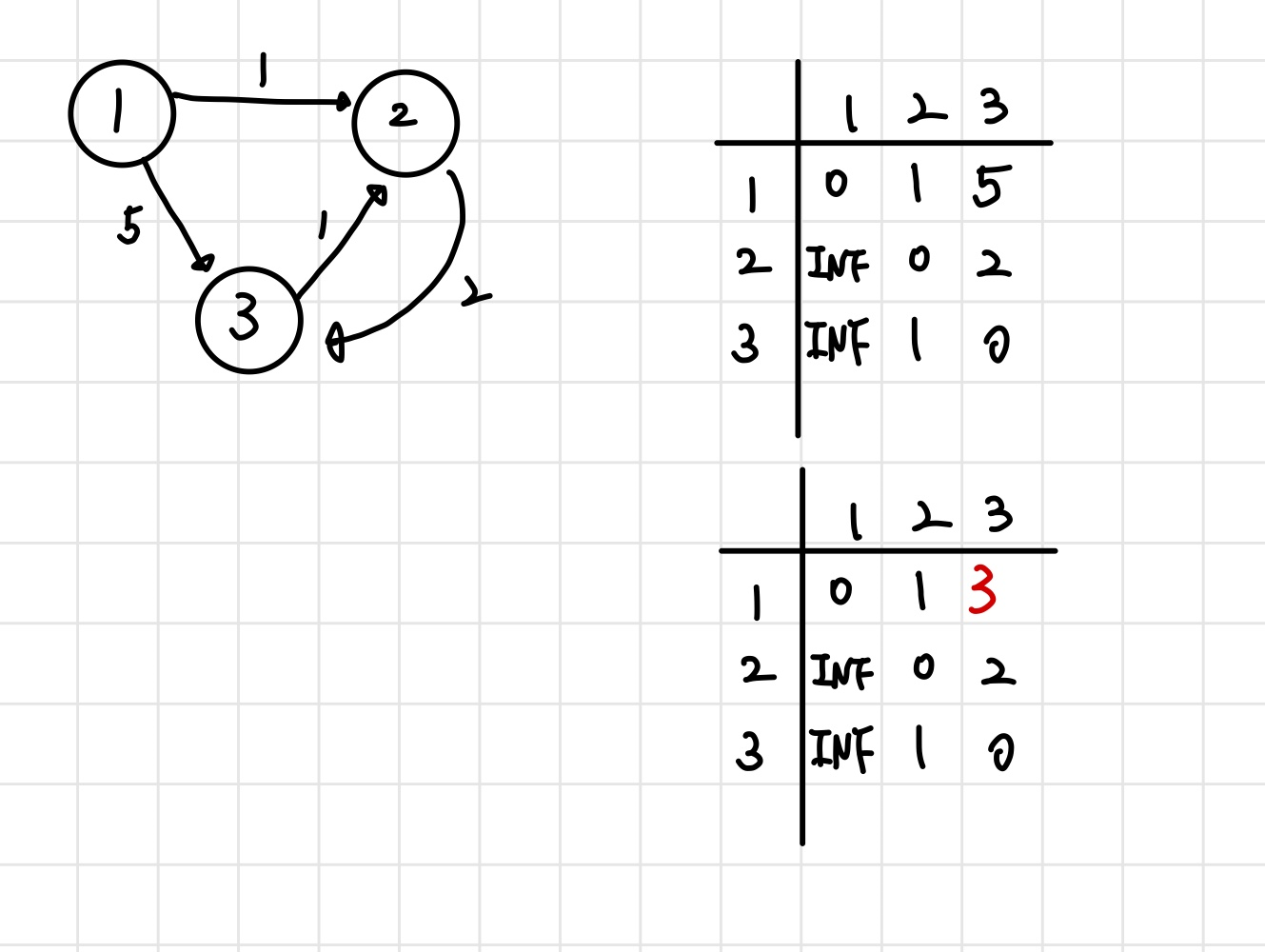
플로이드 워셜 알고리즘은 3중 for문을 돌며
각 노드에서 특정한 노드 k를 거쳐가는 경우를 확인하며 최단거리를 갱신한다.
3중 for문에서 k는 거쳐가는 노드, i는 시작 노드, j는 끝 노드이다.
비교적 간단한 알고리즘인데 3중 for문을 사용하기 때문에
시간복잡도가 O(N**3)이나 된다.
고려할 노드의 수가 적을 때는 상관없지만
그 수가 많아지면 다른 알고리즘을 사용하는 것이 훨씬 효율적일 것이다.
728x90
'자료구조 & 알고리즘 & cs > 알고리즘' 카테고리의 다른 글
| [TIL] 최단 경로 알고리즘 - 벨만 포드 알고리즘 (1) | 2023.05.19 |
|---|---|
| [TIL] - 유클리드 호제 - 최소공배수와 최대공약수 (0) | 2023.05.18 |
| [TIL] 최소 신장 트리(MST) 2 - 프림(prim) 알고리즘 (0) | 2023.05.11 |
| [TIL] 최소 신장 트리(MST) 1 - 크루스칼(kruskal) 알고리즘 (1) | 2023.05.10 |
| [TIL] knapsack 알고리즘 (배낭 문제) (0) | 2023.04.25 |

